FEM-Simulation (Finite-Elemente-Methode)
Was ist FEM?
Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur Berechnung und Analyse von komplexen physikalischen Phänomenen und Strukturen. Sie wird vor allem in den Ingenieurwissenschaften und angewandten Naturwissenschaften eingesetzt, um mechanische, thermische, elektrische oder fluidmechanische Probleme zu lösen.
Was macht FEM?
Die FEM zerlegt ein komplexes Problem in kleinere, einfachere Elemente, die durch mathematische Gleichungen und Modelle beschrieben werden können. Diese Elemente können zum Beispiel Dreiecke oder Rechtecke sein und bilden ein Netzwerk oder Gitter über das gesamte Gebiet, das analysiert werden soll. Jedes Element wird dann durch mathematische Gleichungen und Randbedingungen beschrieben, die die physikalischen Gesetze und das Verhalten des Systems widerspiegeln.
Einsatzgebiete der Finite-Elemente-Analyse
Die Finite-Elemente-Analyse kann für verschiedene Zwecke eingesetzt werden, darunter:
Strukturmechanik
Analyse von Spannungen, Deformationen und Festigkeitsverhalten von Bauteilen und Strukturen unter verschiedenen Belastungen.
Wärmeübertragung
Untersuchung von Temperaturverteilungen und Wärmeleitfähigkeiten in thermischen Systemen und Bauteilen.
Strömungsmechanik
Simulation von Strömungsvorgängen in Fluiden wie Luft oder Flüssigkeiten, um Druckverteilungen, Geschwindigkeiten und Strömungsmuster zu analysieren.
Elektromagnetismus
Berechnung von elektrischen Feldern und Magnetfeldern in elektrischen und magnetischen Systemen.
Was sind die Vorteile der FEM?
Flexibilität
Die FEM kann auf komplexe Geometrien und Materialien angewendet werden und ist daher für eine Vielzahl von Anwendungen geeignet.
Genauigkeit
Durch die Verwendung kleiner Elemente und die Kombination von lokalen Lösungen ergibt sich eine hohe Genauigkeit bei der Lösung komplexer Probleme.
Anwendbarkeit
Die FEM kann in Verbindung mit Computersimulationen verwendet werden, um realistische Vorhersagen zu treffen und das Verhalten von komplexen Systemen zu verstehen.
Was ist eine FEM-Simulation?
Eine FEM-Simulation (Finite-Elemente-Methode-Simulation oder auch Finite-Elemente-Simulation) ist eine computergestützte numerische Analyse, die auf der Finite-Elemente-Methode (FEM) basiert. Sie wird verwendet, um das Verhalten von komplexen physikalischen Phänomenen und Strukturen zu analysieren und vorherzusagen. In einer FEM-Simulation wird das zu untersuchende Gebiet in kleinere, einfachere Elemente unterteilt, die durch mathematische Gleichungen und Modelle beschrieben werden können.
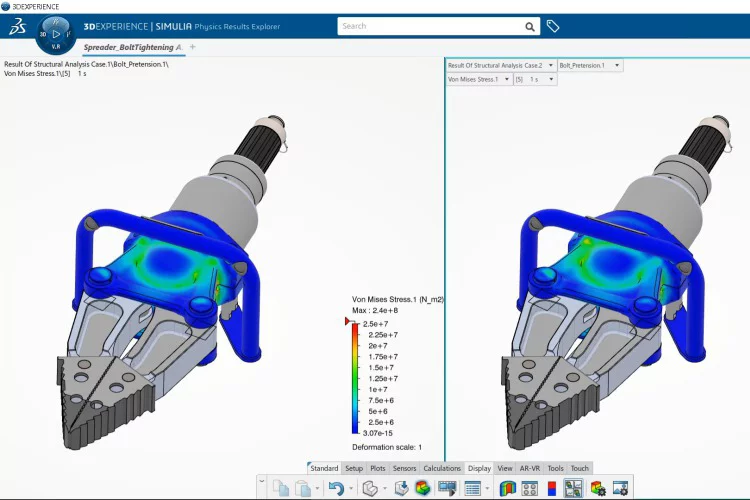
Warum FEM-Simulation?
Die Finite-Elemente-Methode wird aus verschiedenen Gründen für Simulationen eingesetzt. Hier sind einige der Hauptvorteile und Gründe, warum FEM-Simulationen in vielen Branchen und Anwendungsbereichen so verbreitet sind:
Komplexität bewältigen: FEM-Simulationen ermöglichen die Analyse und Vorhersage des Verhaltens komplexer physikalischer Phänomene und Strukturen. Sie können in Situationen angewendet werden, in denen analytische Lösungen nicht praktikabel oder sogar nicht verfügbar sind.
Effizienz und Kostenersparnis: Durch FEM-Simulationen können Ingenieure und Wissenschaftler virtuelle Prototypen erstellen und deren Verhalten unter verschiedenen Bedingungen analysieren, ohne physische Prototypen erstellen zu müssen. Dies spart Zeit, Materialkosten und Entwicklungsressourcen.
Designoptimierung: FEM-Simulationen ermöglichen es, verschiedene Designoptionen zu analysieren und zu vergleichen, um das bestmögliche Design zu finden, das den Anforderungen und Spezifikationen am besten entspricht. Dies trägt zur Verbesserung der Leistung, Sicherheit und Effizienz von Produkten und Strukturen bei.
Vorhersage von Verhalten: FEM-Simulationen ermöglichen es, das Verhalten von Bauteilen und Strukturen unter verschiedenen Belastungen und Bedingungen vorherzusagen. Dies kann dazu beitragen, potenzielle Probleme frühzeitig zu erkennen und die notwendigen Anpassungen oder Verbesserungen vorzunehmen, bevor ein Produkt auf den Markt kommt.
Nichtlineares Verhalten: FEM-Simulationen können auch nichtlineares Verhalten modellieren, das in vielen praktischen Anwendungen vorkommt. Dazu gehören Materialverformungen, große Verschiebungen, komplexe Randbedingungen und andere Phänomene, die in der Realität auftreten können.
Verständnis komplexer Systeme: Durch FEM-Simulationen können Ingenieure und Wissenschaftler ein besseres Verständnis von komplexen Systemen und physikalischen Prozessen gewinnen. Dies kann zu neuen Erkenntnissen und Innovationen führen.
Sicherheit und Zuverlässigkeit: FEM-Simulationen spielen eine wichtige Rolle bei der Bewertung der Sicherheit und Zuverlässigkeit von Produkten und Strukturen. Sie können helfen, potenzielle Schwachstellen zu identifizieren und die Sicherheit für Endnutzer zu gewährleisten.
Insgesamt ermöglicht die Finite-Elemente-Methode mit ihren Simulationen eine leistungsfähige Werkzeugpalette, um komplexe technische Herausforderungen zu bewältigen, die Leistung zu optimieren, das Verständnis von physikalischen Phänomenen zu vertiefen und letztendlich die Qualität und Effizienz von Produkten und Strukturen zu verbessern.
Der Ablauf einer FEM-Simulation
Geometriemodellierung: Das zu analysierende Objekt oder System wird in einem virtuellen 3D-Modell repräsentiert. Die Geometrie wird in kleinere Elemente, wie Dreiecke oder Rechtecke, unterteilt, um ein Netzwerk oder Gitter zu bilden.
Definition von Materialeigenschaften und Randbedingungen: Für jedes Element werden die Materialeigenschaften (z. B. Elastizität, Wärmeleitfähigkeit) und die Randbedingungen (z. B. Kräfte, Temperaturen) festgelegt, die auf das Element einwirken oder es begrenzen.
Formulierung der Gleichungen: Für jedes Element werden Gleichungen entwickelt, die die physikalischen Gesetze und das Verhalten des Elements beschreiben. Diese Gleichungen können unterschiedlich sein, abhängig von der Art der zu simulierenden Phänomene (z. B. mechanische Spannungen, Wärmeübertragung, Strömungsverhalten).
Zusammenbau und Lösung des Gleichungssystems: Alle Gleichungen der Elemente werden zu einem großen Gleichungssystem zusammengefügt und gelöst, um das Verhalten des gesamten Systems zu simulieren. Dies erfordert häufig die Verwendung von leistungsstarker Computerhardware und spezieller Software für die numerische Berechnung.
Analyse der Ergebnisse: Nach Abschluss der Simulation werden die Ergebnisse analysiert und interpretiert. Dies kann umfassen, die Verteilung von Spannungen, Temperaturen, Strömungsgeschwindigkeiten oder anderen physikalischen Größen zu visualisieren und zu verstehen.
FEM-Simulationen werden in vielen verschiedenen Branchen eingesetzt, darunter Ingenieurwesen, Maschinenbau, Bauwesen, Automobilindustrie, Luft- und Raumfahrt, Medizintechnik und viele andere. Sie ermöglichen es Ingenieuren und Wissenschaftlern, das Verhalten von Produkten und Strukturen vorherzusagen, die Auswirkungen von Designänderungen zu analysieren, die Leistung zu optimieren und potenzielle Probleme frühzeitig zu identifizieren, bevor physische Prototypen erstellt werden. Dies trägt zur Effizienz, Sicherheit und Zuverlässigkeit von Produkten und Strukturen bei und ermöglicht es, komplexe Systeme besser zu verstehen und zu verbessern.
Verbindung von FEM und CAD
FEM und CAD sind eng miteinander verbunden. CAD-Modelle dienen als Ausgangspunkt für FEM-Simulationen. Die geometrischen Informationen und Materialeigenschaften aus den CAD-Modellen werden in die FEM-Simulationssoftware übertragen, um die physikalischen Analysen durchzuführen. Die Ergebnisse der FEM-Simulationen können dann wiederum in die CAD-Modelle zurückgeführt werden, um das Design entsprechend zu optimieren oder anzupassen. Die Kombination von FEM und CAD ermöglicht es Ingenieuren und Designern, Produkte und Strukturen effizienter zu entwickeln, zu analysieren und zu verbessern.
FEM-Software
FEM-Software sind spezialisierte Tools, die Ingenieuren und Wissenschaftlern ermöglichen, das Verhalten von Strukturen unter verschiedenen Belastungsbedingungen zu simulieren, zu analysieren und zu optimieren. Diese Softwarelösungen verwenden numerische Methoden wie die Finite-Elemente-Methode (FEM) oder die Finite-Differenzen-Methode, um komplexe mathematische Modelle von Strukturen zu erstellen. Hier sind einige bekannte Softwarepakete für die Strukturanalyse:
SOLIDWORKS Simulation
SOLIDWORKS Simulation ist ein anwenderfreundliches Portfolio an Werkzeugen zur Strukturanalyse. Dabei wird die Finite-Elemente-Methode (FEM) eingesetzt, um anhand virtueller Tests von CAD-Modulen das tatsächliche physikalische Verhalten eines Produkts vorherzusagen. Das Portfolio umfasst lineare, nichtlinear-statische und dynamische Analysen.
3DEXPERIENCE Works Simulation
Die Struktursimulation aus 3DEXPERIENCE Works beinhaltet leistungsstarke, kollaborative und vernetzte Simulationslösungen auf der Cloud-basierten 3DEXPERIENCE®-Plattform. Sie können Konstruktionsinnovationen beschleunigen durch volle Daten-Assoziativität beim Lösen technischer Herausforderungen Ihrer SOLIDWORKS 3D Konstruktionen.
ABAQUS
SIMULIA Abaqus Unified FEA liefert etablierte, hochleistungsfähige FEA-Simulationslösungen für komplexe nichtlineare Probleme, umfangreiche lineare Dynamikanalysen, Multiphysiksaufgaben sowie für Routineaufgaben. Mit der Abaqus Suite lassen sich vollständige Fahrzeuglasten, dynamische Vibrationen, Crash, Mehrkörpersysteme, nichtlineare Statik, thermische Kopplung und akustisch-strukturelle Kupplung mit nur einer Modellierungsdatenstruktur und integrierter Solver-Technologie betrachten.
Fazit
Die Finite-Elemente-Methode hat die Ingenieurwissenschaften und andere angewandte Wissenschaften revolutioniert, da sie es ermöglicht, reale Probleme in virtuellen Umgebungen zu analysieren, ohne aufwendige und teure Experimente durchführen zu müssen. Sie ist zu einem unverzichtbaren Werkzeug in der modernen Forschung und Industrie geworden, um die Leistung und Zuverlässigkeit von Produkten und Strukturen zu verbessern.