Tipps & Tricks
Keine Angst vor dynamisch-expliziten Berechnungen.
Wir zeigen Ihnen, wie dynamisch-explizite Berechnungen mit Abaqus die explizite Zeitintegration zur Analyse hochdynamischer Vorgänge und großer Deformationen nutzen. Sie sind besonders effizient für kurze, transiente Ereignisse wie Crash-Simulationen, Zugversuche oder Überdrucksimulationen.
10.12.24
Vielleicht haben Sie das auch schon mal gesehen: Ein Handy fällt, realistisch simuliert auf den Boden und zerbricht wie in echt in seine Einzelteile. Oder der Klassiker: Ein Fahrzeug in der Entwicklung im Crashtest – der Airbag platzt auf, Dummies werden aus dem Sitz geschleudert – alles realistisch simuliert. Wie funktioniert das?
Möglicherweise haben Sie schon einmal mit SOLIDWORKS Simulation Premium versucht, einen einfachen Falltest zu simulieren – aber die ganze „Power“ des expliziten Solvers bekommen Sie erst mit SIMULIA Abaqus!
Fangen wir mit ein paar Grundlagen an: Die implizit statische Berechnung ist ja in der Regel bekannt – die Grundgleichung ist hier wie in meinem letzten Blogbeitrag „CAE-Modelle checken mit Eigenmoden“ beschrieben, die lineare oder nichtlineare Federgleichung. Der explizite Solver verwendet als Grundgleichung das zweite Newtonsche Gesetz in Matrixschreibweise für konstante Massen:
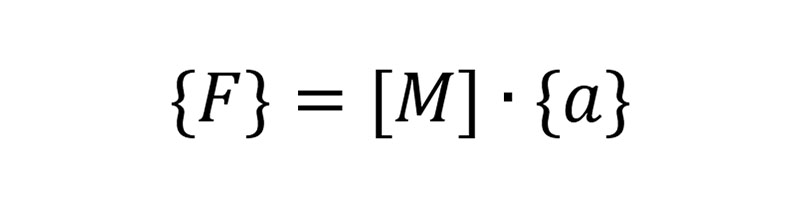
mit:
{F}: Vektor aller Knoten – Kräfte
[M]: System – Massen – Matrix
{a}: Vektor aller Knoten – Beschleunigungen
Zusätzlich erhalten wir aus dem Weg-Zeit-Gesetz den Zusammenhang zwischen Beschleunigung und Verschiebung (Weg):
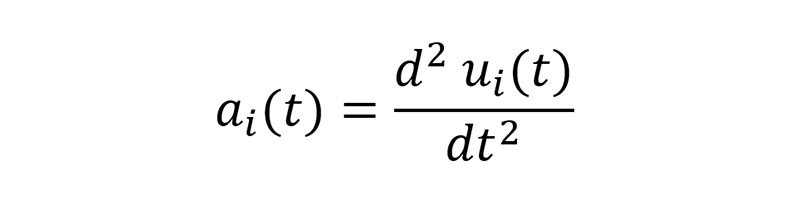
i-te Beschleunigung = 2. Ableitung nach der i-ten Verschiebung
An diesen zwei Formeln sehen Sie schon, dass wir einen ganz anderen mathematischen Ansatz als in der Statik verwenden.
Wir gehen von folgender Vorstellung aus:
Durch das Modell läuft eine Deformationswelle mit der Schallgeschwindigkeit des Materials, welche von Element zu Element läuft und jedes (Massen-)Element erfassen muss.
Das Verhalten kann man sich gut wie einen Mehrmassen-Schwinger vorstellen, vergleiche Abbildung 1.
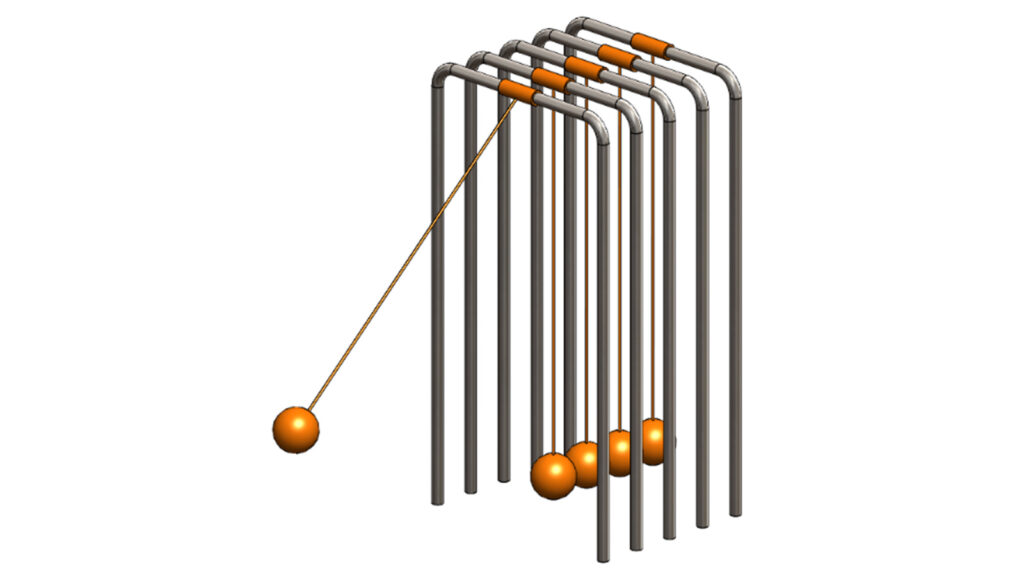
Abbildung 1: Mehrmassenschwinger (aus SOLIDWORKS Motion Schulung)
Für jede dynamisch-explizite Berechnung gilt damit:
Alles, was sich bewegt, muss eine Masse und eine Massenträgheit haben. Bei verformbaren Körpern kann sich Abaqus diese aus Geometrie bzw. Volumen und Dichte berechnen, d. h. Sie müssen beim Materialverhalten immer eine Materialdichte angeben.
Zuerst werden vom expliziten Solver die Knoten-Beschleunigungen berechnet – nicht die Knotenverschiebungen wie in der Statik(!). Über die Verrechnung mit der Masse erhalten Sie daraus sofort die Knotenkräfte. Anschließend werden über Integration über das Elementvolumen die Spannungen bzw. andere Elementergebnisse berechnet.
Für die Bestimmung der Knoten-Verschiebungen müssen Sie dann zunächst die Knoten-Beschleunigungen zweimal über die Zeit integrieren. Diese sind daher – im Gegensatz zu einer statischen Berechnung – sehr abhängig von der Qualität der Vernetzung.
Infolge der schnellen Energieumwandlung, z. B. von Bewegungsenergie bzw. kinetischer Energie in Verformungsenergie, sollten Sie immer die Energiebilanzen (äußere, innere, kinetische Energie etc.) kontrollieren.
Meist werden in kurzer Zeit große Verformungen erreicht, wie beispielsweise bei einem Fahrzeug-Crash, sodass in der Regel mit geometrisch nichtlinearen und großen lokalen Verformungen gerechnet wird.
Der Zeitschritt.
Als Grundelement der expliziten Berechnung erhalten wir damit – folgernd aus der Newtonschen Grundgleichung und dem Weg-Zeit-Gesetz (s. o.) – den sogenannten „Zeitschritt dt“. In jedem kleinen Zeitschritt dt läuft Ihre Deformationswelle z. B. der Stoß beim Aufprall auf eine Ecke, maximal ein Element weiter. Der kleinste Zeitschritt, mit dem der Solver rechnen muss, damit alle Elemente von der Deformationswelle sicher erfasst werden, errechnet sich dabei aus der Material-Schallgeschwindigkeit und der kleinsten Elementlänge im gesamten Modell.
Bei der expliziten Berechnung geht es also nicht um Gleichgewichtsbedingungen und Matrixinversion – wie bei einer implizit-statischen Berechnung – sondern vielmehr um die Berechnung von sehr vielen, sehr kleinen Zeitschritten der Größe:

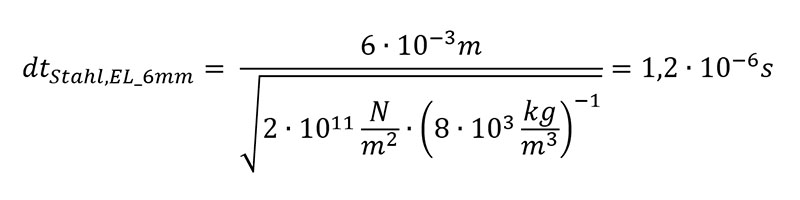
Da Sie sehr viele kleine Berechnungen ausführen, benötigen Sie für die explizite Berechnung einen schnellen Rechner – Arbeitsspeicher ist da nicht so relevant wie Rechenleistung – mit vielen Kernen, um ein komplexes Problem parallel rechnen zu können. Kontakte sind wegen der kleinen Schrittweiten zumeist unproblematisch.
Wo die Statik versagt, können Sie immer dynamisch mit realen Massen und Beschleunigungen und realer Zeit(!) dynamisch-explizit rechnen. Allerdings hätten Sie bei Stahl, siehe Beispiel oben mit der Schallgeschwindigkeit c_Stahl ≈ 6000 m/s und ca. 6 mm kleinster Elementlänge (EL) einen Zeitschritt von nur dt = 1e-6 s – es müssten also bei 1s Rechenzeit ca. 1 Million(!) Zeitschritte vom Solver berechnet werden. Daher werden explizit zumeist nur sehr kurze Vorgänge berechnet. Auch beim Herausschreiben der Ergebnisse sollten Sie sich auf die relevanten Ergebnisse beschränken, da sonst sehr große odb-Dateien (Output-Data Base, dt. Ergebnisdatei) von vielen GB entstehen. Anzumerken ist hier, dass gerade Abaqus auch große Ergebnisdateien von 10 GB und mehr problemlos, flüssig und schnell verarbeiten kann.
Mass-Scaling, was ist das?
Gegen zu lange Rechenzeiten infolge zu kleiner Elemente hilft Mass-Scaling. Beim Mass-Scaling wird auf zu kleine (unwichtige) Elemente künstlich Masse „draufgepackt“, um einen bestimmten minimalen Zeitschritt für das gesamte Modell nicht zu unterschreiten. Aber Vorsicht zu viel Mass-Scaling kann insbesondere bei sehr schnellen Vorgängen, bei denen Massen und Massenträgheiten eine wichtige Rolle spielen, zu verfälschten Ergebnissen führen – hier gilt es abzuwägen.
Wann punktet der explizit dynamische Solver?
Bei allen crashartigen Stoß- und hochdynamischen Vorgängen müssen Sie dynamisch rechnen. Vor allem bei allen sehr kontaktlastigen, dynamischen Berechnungen empfiehlt sich ebenso der explizite Solver, insbesondere auch bei Selbstkontakt. Letzteres kann vorkommen, wenn sich Strukturen so sehr zusammenfalten oder beulen, dass die verformte Geometrie sich selbst wieder berührt, vergleiche Abbildung 3 und Video 1.
Bei allen Berechnungen, bei denen sich die Element-Steifigkeit deutlich ändert, bei Umformprozessen und insbesondere bei (Ab)Reißen, (Ab)Scheren, Platzen und anderen Versagensberechnungen, empfiehlt sich immer der dynamisch-explizite Solver.
Weiterhin lassen sich Struktur-Flüssigkeitsinteraktionen, Partikelberechnungen und transiente Wärmeübertragung uvm. berechnen.
Wie mache ich das in Abaqus/CAE?
Abaqus/CAE steht für Complete Abaqus Environment. Das heißt, dass Sie z. B. problemlos zwischen dem impliziten und dem expliziten Solver wechseln können. Sie müssen lediglich das hier anpassen:
Step à Umstellen (replace) explizit-dynamisch
Kontakt à i. d. R. General Contact (explicit) – allgemeiner Bauteilkontakt und
Elementtyp à Solver-geeignete Elemente wählen und
Vernetzung à nicht zu feines (Zeitschritt sinkt!), gleichmäßiges, qualitativ hochwertiges Netz.
Beispiel aus dem Automotive-Bereich: „Vereinfachter Pfahl-Crash“.
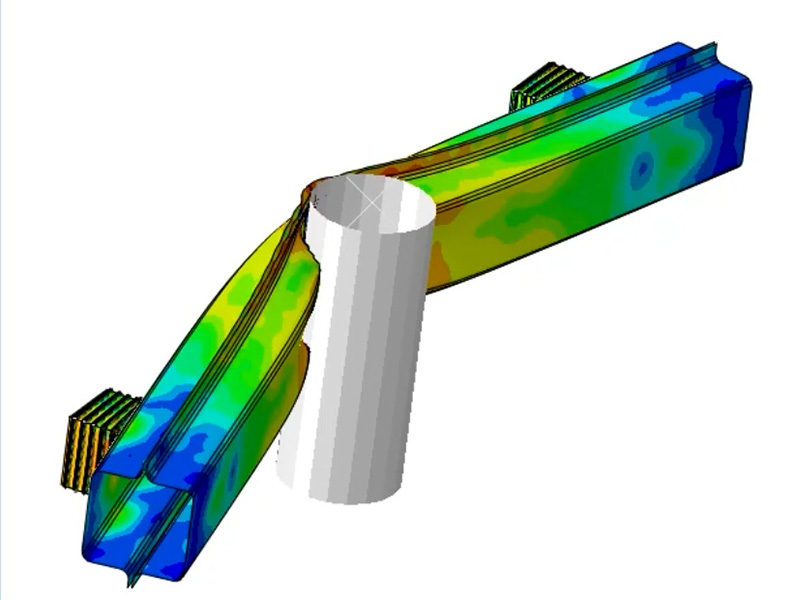
Schauen wir uns ein Beispiel aus dem Automotive-Bereich an – eine vereinfachte Pfahl-Crash-Analyse – hier halbsymmetrisch berechnet:
Das Modell besteht aus einem Querträger (Stoßfänger) mit Crash-Can. Letzteres ist ein Falt-Element, welches die Stoßenergie des Aufpralls absorbiert.
Der Pfahl, hier vereinfacht modelliert als starrer Körper, kollidiert mit der Fahrzeug-Frontstruktur (Masse: 2000 kg, ca. 200 g als Crash-Beschleunigung) in 0.025 s – reduziert auf Stoßstangen-Querträger und Crash-Can.
Für die dynamisch-explizite Berechnung sollten Sie nicht zu fein vernetzen. Kleine unwichtige Geometrie-Features werden dazu in aller Regel unterdrückt, um eine sehr gute und qualitativ hochwertige Vernetzung zu erhalten. Dünnwandige Strukturen sollten mit Schalen vernetzt werden.
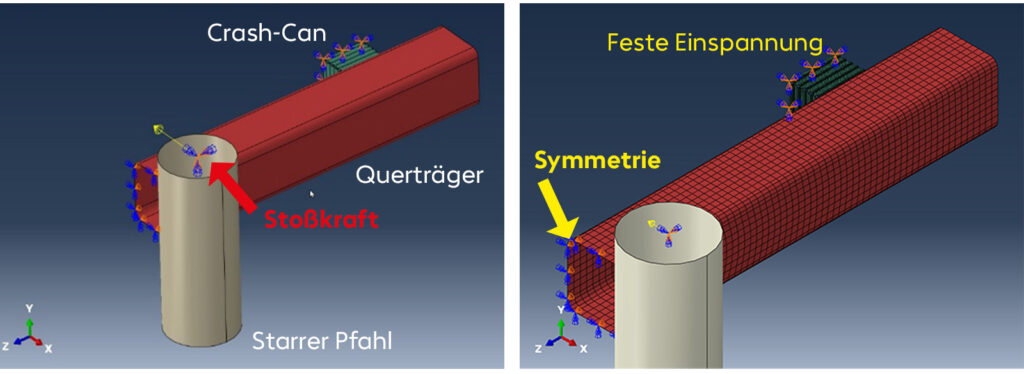
Abbildung 2: Crash-Beispiel, links mit Randbedingungen, rechts mit Vernetzung
Step: Stellen Sie den Step auf dynamic-explicit mit 0.025 s = 25 ms Stepzeit und zunächst einem Mass-Scaling (minimaler Zeitschritt) von 1e-6 s ein.
Randbedingung: Randbedingungen für Halbsymmetrie, der Pfahl bewegt sich geradlinig (Querträger unbewegt).
Last: Die Stoßkraft beträgt 200 g *1000 kg (halbes Fahrzeug) = 2000 kN = 2e6 N, mit einer linearen Amplitude von 0 bis 0.025 s.
Kontakt: im Initial Step à General Contact (explicit) – Reibung: fric=0.1 (Penalty)
Elementtyp-Optionen à geeignet für expliziten Solver, z. B. quadratische TETRA- und lineare HEXA-Elemente oder lineare oder quadratische SHELL-Elemente.
Das Ergebnis – hier zusätzlich mit Versagen der Schweißverbindungen zwischen Crash-Can und Querträger – zeigt klar Einbeulen und die massive Verformung des Querträgers in weniger als 15 ms.
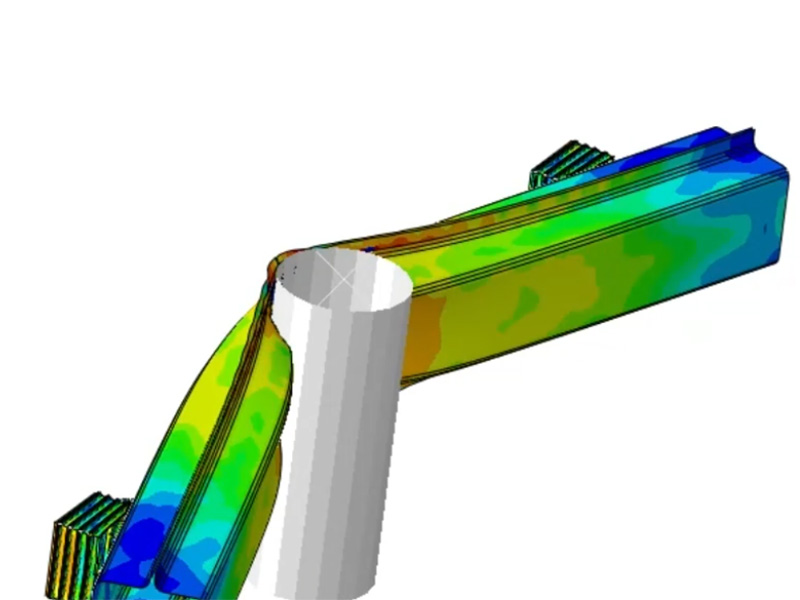
Abbildung 3: Verformung des Querträgers beim Pfahl-Crash
Video 1: Beispiel Pfahl-Crash
Beispiel aus dem Bereich Materialtests: „Zugversuch für eine Rundprobe“.
Als zweites Beispiel zeige ich Ihnen einen rotationssymmetrisch gerechneten Zugversuch, den der explizite Solver auch problemlos mit Anreißen und Brechen rechnet. Die eingebaute duktile Schädigung kann entweder über die exakten Materialdaten oder wie hier vereinfacht als linearer Abfall der Spannungs-Dehnungskurve gerechnet werden. Die Elementsteifigkeit wird im Falle des Erreichens einer kritischen plastischen Dehnung EPScrit von K0=100% auf z. B. 20% linearheruntergefahren. „Versagende“ Elemente werden dann herausgelöscht, was schließlich einen Riss entstehen lässt – siehe Abbildung 4 (rechts).
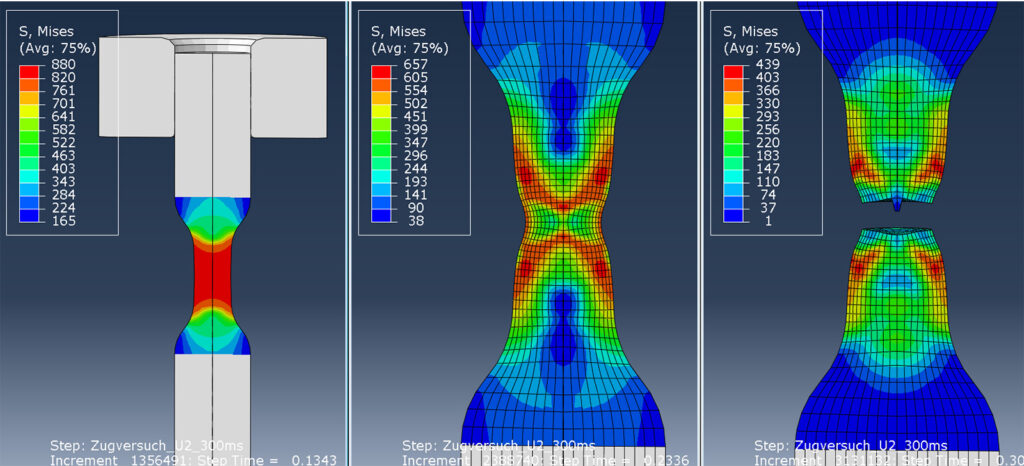
Abbildung 4: Ergebnis: Zugversuch mit duktiler Schädigung; Einschnürung (Mitte) und Reißen (rechts)
Beispiel aus dem Bereich Komponententests: „Berstversuch eines Druckbehälters“.
Zum Abschluss zeige ich hier noch den Berstversuch eines Druckbehälters, wiederum mit duktiler Schädigung modelliert: Der Druck in einem Behälter (Schalenstruktur, Viertelmodell) wird erhöht, bis der Behälter schließlich platzt, was gut in der Bildfolge zu erkennen ist.
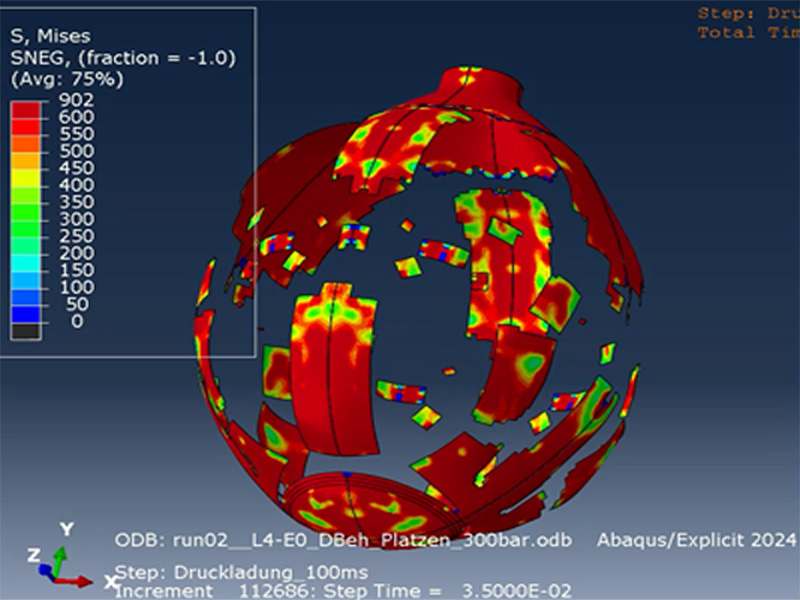
Abbildung 5: Berstender Druckbehälter
Video 2: Berstversuch eines Druckbehälters
Fazit
Mit dem dynamisch-expliziten Solver haben Sie in SIMULIA Abaqus ein sehr mächtiges, hochinteressantes und äußerst vielseitiges Werkzeug, welches immer funktioniert, wenn der implizite Solver keine Konvergenz mehr findet, z. B. weil sich Teile frei bewegen oder Steifigkeiten massiv verändern. In Abaqus/CAE kann schon mit wenigen Clicks eine implizit-statische Analyse in eine explizit-dynamische Berechnung umgebaut werden.
Kategorien
Allgemein Neuigkeiten Ratgeber Tipps & Tricks
Zum Bechtle PLM News-Service anmelden.
Keine Neuigkeiten, Tipps & Tricks, Events u.v.m. rundum Engineering & Manufacturing mehr verpassen.
Weitere Beiträge
Sie haben Fragen? Sprechen Sie uns an!
Wir sind hier, um Ihnen zu helfen! Schicken Sie uns Ihre Frage über das nebenstehende Formular.
Ihre Zufriedenheit hat oberste Priorität. Wenn Sie Informationen benötigen, Unklarheiten haben oder spezifische Anliegen besprechen möchten, zögern Sie nicht, uns zu kontaktieren. Füllen Sie einfach das Formular aus, wir werden uns schnellstmöglich bei Ihnen melden. Vielen Dank für Ihr Vertrauen!


