Große Modelle, einfache Lösungen. Substrukturtechnik in der FEM.

Mit dem Aufkommen der Computertechnologie übernahmen Rechner zunehmend die Lösung großer und komplexer Probleme, während Ingenieur:innen einfache Berechnungen weiterhin manuell durchführten. Doch schnell zeigte sich, dass der steigende Bedarf an Rechenkapazität oft die Möglichkeiten der verfügbaren Hardware überstieg. Dieser Kreislauf setzte sich über die Jahre fort: Immer wenn die Rechenleistung stieg, wurde sie bald von noch komplexeren technischen Aufgaben überholt.

Substrukturtechnik als Antwort auf limitierte Ressourcen.

Heute können moderne Computersysteme Millionen von Gleichungen bewältigen, was jedoch für viele Ingenieur:innen noch nicht genug ist. Die Grenze der Hardwareressourcen sowie die hohen Kosten und der zeitliche Aufwand, die solche Berechnungen verursachen, stellen nach wie vor eine Herausforderung dar. Eine effektive Lösung hierfür ist die Anwendung der Substrukturtechnik, die es ermöglicht, große Berechnungen in kleinere, handhabbare Teilaufgaben zu zerlegen und so den Hardwarebedarf zu reduzieren.

Was ist Substrukturtechnik? Erläuterung am Beispiel eines Tischmodells in SIMULIA Abaqus.

Die Substrukturtechnik ist eine Methode, die bei Modellen mit wiederkehrenden Teilstrukturen oder häufig wiederverwendeten Modellteilen mit linearem Verhalten angewendet werden kann. Als Beispiel betrachten wir einen Tisch, der aus einer Platte und vier identischen Beinen besteht. Da die Verformung der Platte unter Druck von Interesse ist und die Steifigkeit der Beine identisch ist, können die Beine (hier mit 3d-Solids modelliert) als Substruktur modelliert werden, wie in Abbildung 1 gezeigt.

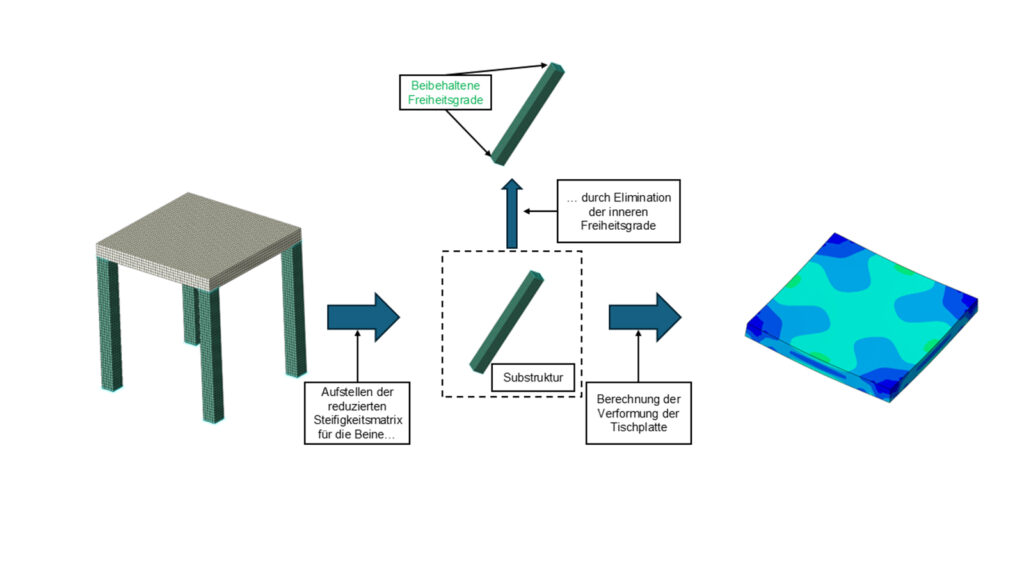
Abbildung 1: Anwendung der Substrukturtechnik

Ziel der Substrukturtechnik ist es, die inneren Freiheitsgrade der Substruktur, die für die Interaktion mit anderen Elementen oder Modellteilen nicht erforderlich sind, vorab aus den Gleichungen zu entfernen. Nur die Freiheitsgrade an den Verbindungs- oder Kopplungsknoten zu anderen Teilmodellen bleiben erhalten. Bei dem oben gezeigten Tisch-Beispiel müssen die Freiheitsgrade der Tischbeine an beiden Enden erhalten werden: einerseits dort, wo die Beine mit der Tischplatte verbunden sind, und andererseits dort, wo die Beine fixiert werden. Das Ergebnis ist eine reduzierte Steifigkeitsmatrix, die nur einmal berechnet werden muss und mit der die Verformung der Tischplatte bestimmt werden kann.

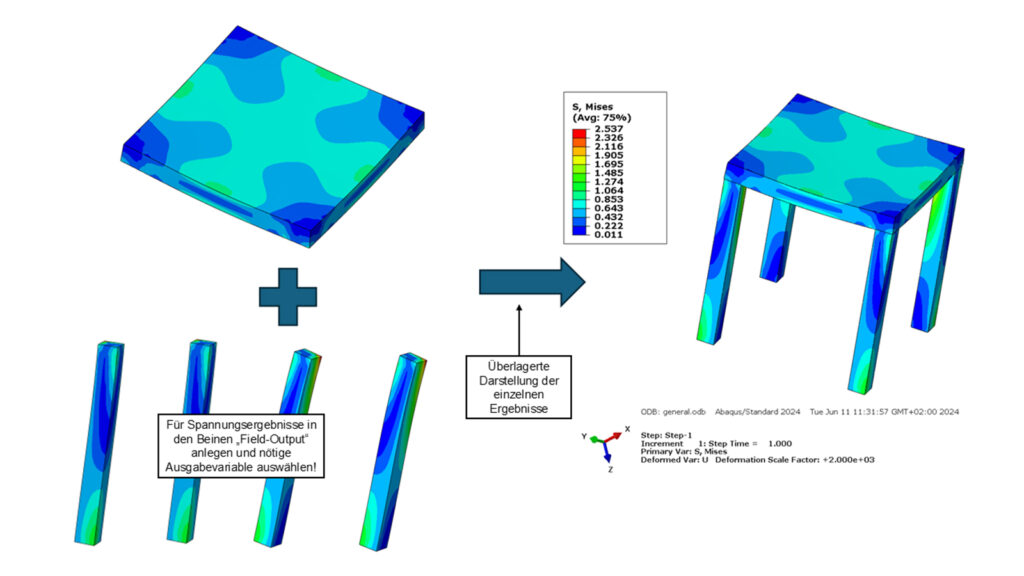
Bei Bedarf können außerdem die zuvor eliminierten Verschiebungsvektoren sowie die daraus resultierenden Elementkräfte und -spannungen für die Tischbeine (siehe Abbildung 2) ermittelt werden. Wichtig ist hierbei, dass für die Berechnung der Spannungen in den Tischbeinen ein entsprechender „Field-Output“ in SIMULIA Abaqus erstellt wird und die benötigten Ausgangsvariablen (z.B. Spannung) ausgewählt werden.

Abbildung 2: Substrukturtechnik FEM: Zusammengeführtes Ergebnis

Wichtig!
Substrukturen können nicht direkt in einer expliziten Simulation verwendet werden. Durch Co-Simulationstechniken (Kopplung von Abaqus/Standard & Explicit) ist dies jedoch indirekt möglich.
Dabei wird der Teil des Simulationsmodells, der die Substruktur darstellt in Abaqus/Standard und der restliche Teil in Abaqus/Explicit modelliert. So entstehen eigenständige INPUT-Dateien und eigenständige Modelle für die Interaktion.

Wesentliche Vorteile der Substrukturtechnik.

1. Reduzierte Systemmatrizen und effizientere Berechnung.

Die Systemmatrizen (Steifigkeit, Masse) sind klein. In der Analyse werden nur die erhaltenen Freiheitsgrade sowie die entsprechende reduzierte Steifigkeits- oder Massenmatrix verwendet.
Die Lösung innerhalb der Substruktur wird erst bei Bedarf wiederhergestellt.

2. Wiederverwendbarkeit von Substrukturen.

Die Effizienz dieser Methode wird besonders deutlich, wenn dieselbe Substruktur mehrfach verwendet wird. Die Berechnung der Steifigkeit und die Reduktion müssen nur einmal durchgeführt werden. Danach kann die Substruktur wiederholt eingesetzt werden, was den Rechenaufwand erheblich verringert.

3. Effiziente Lösung bei lokalen Nichtlinearitäten.

Bei Problemen mit lokalen Nichtlinearitäten, wie z.B. bei Modellen mit Grenzflächen, die Trennung oder Berührung erfahren können, können die Iterationen zur Lösung dieser Nichtlinearitäten deutlich effizienter gestaltet werden. Dies wird erreicht, indem die Substrukturtechnik genutzt wird, um das Modell auf die Freiheitsgrade zu reduzieren, die direkt an den lokalen Nichtlinearitäten beteiligt sind. Auf diese Weise können die Berechnungen mit einer wesentlich geringeren Anzahl von Freiheitsgraden durchgeführt werden. Da die Substruktur nur aus einer Gruppe erhaltener Knotenfreiheitsgrade besteht, hat sie keine Oberflächengeometrie, um eine Kontaktfläche zu definieren. Um dennoch einen Kontakt zu definieren, muss die Außenseite der Substruktur z. B. mit Flächenelementen oder Strukturelementen vernetzt werden, oder es muss eine “node-based”- Oberfläche oder ein Kontaktelement definiert werden.

Substrukturen in SIMULIA Abaqus.
So setzen Sie sie erfolgreich um.

1. Modellierung und Definition des Substruktur-Bereichs
(Modell Substruktur).

• Geometrie und Materialdefinition
  Erstellen Sie im „PART“-Modul die Geometrie des Tischbeins. Definieren Sie anschließend die Materialeigenschaften und die “Section” im „PROPERTY“-Modul und ordnen Sie das Material der “Section” zu.

• Baugruppe im “ASSEMBLY”-Modul
  Laden Sie die Substruktur als Instanz im „ASSEMBLY“-Modul.

2. Substruktur-Lastschritt “Substructure generation” erstellen.

• Lastschritt definieren
  Legen Sie im „STEP“-Modul einen Berechnungsschritt an, der die reduzierte Steifigkeit und Masse der Substruktur berechnet. (1) + (2)

• Substruktur-Identifier definieren
  Definieren Sie einen eindeutigen Bezeichner unter „Substructure Identifier“ für die Substruktur, die nach dem Buchstaben „Z“ benannt wird. Dieser Identifier wird im Namen der Importdatei (SIM) gespeichert und erleichtert die Identifikation in Modellen mit mehreren Substrukturen. (3)

• Recovery Region festlegen
  Legen Sie die Region fest, deren eliminierte Freiheitsgrade wiederhergestellt werden sollen, um Spannungen und Dehnungen innerhalb der Unterstruktur zu berechnen. Wählen Sie entweder die gesamte Substruktur („Whole Region“) oder spezifische Knoten-/Elementgruppen. (4)

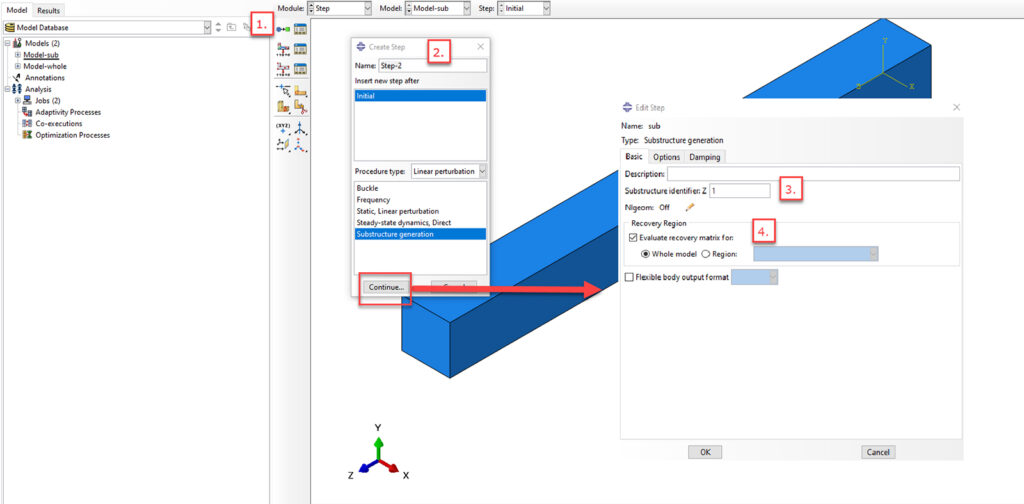
Abbildung 3: Substrukturtechnik FEM: Einstellung des Substruktur-Lastschritts

3. Vernetzung.

• Vernetzen Sie den Bereich, der als Substruktur verwendet werden soll, im Modul „MESH“.

4. Definition der Freiheitsgrade, die erhalten bleiben sollen (Retained DOFs).

• Schnittstellenknoten definieren: Erstellen Sie im „ASSEMBLY“-Modul ein Node-Set, das die Knoten enthält, die als Schnittstellen zum Hauptmodell dienen. Diese Knoten repräsentieren die „Retained Degrees of Freedom“.

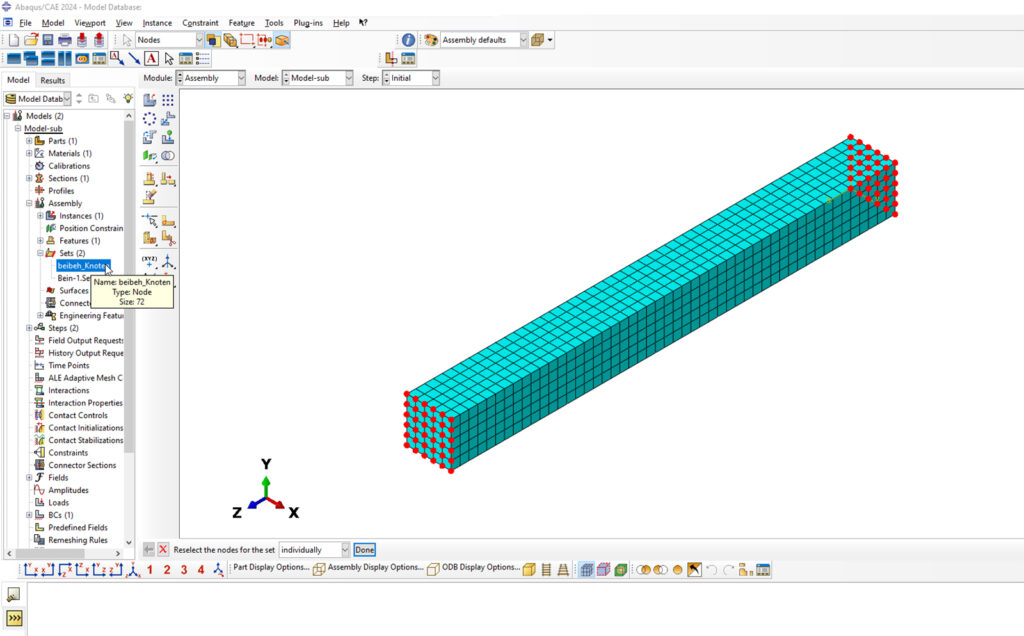
Abbildung 4: Substrukturtechnik: Die Verbindungs- bzw. Kopplungsknoten im Node-Set

• Randbedingung festlegen: Weisen Sie im Modul „LOAD“ die Randbedingung „Retained nodal DOFs“ den im Node-Set enthaltenen Kopplungsknoten zu. Wählen Sie die drei translatorischen Freiheitsgrade, die beibehalten werden sollen, aus.

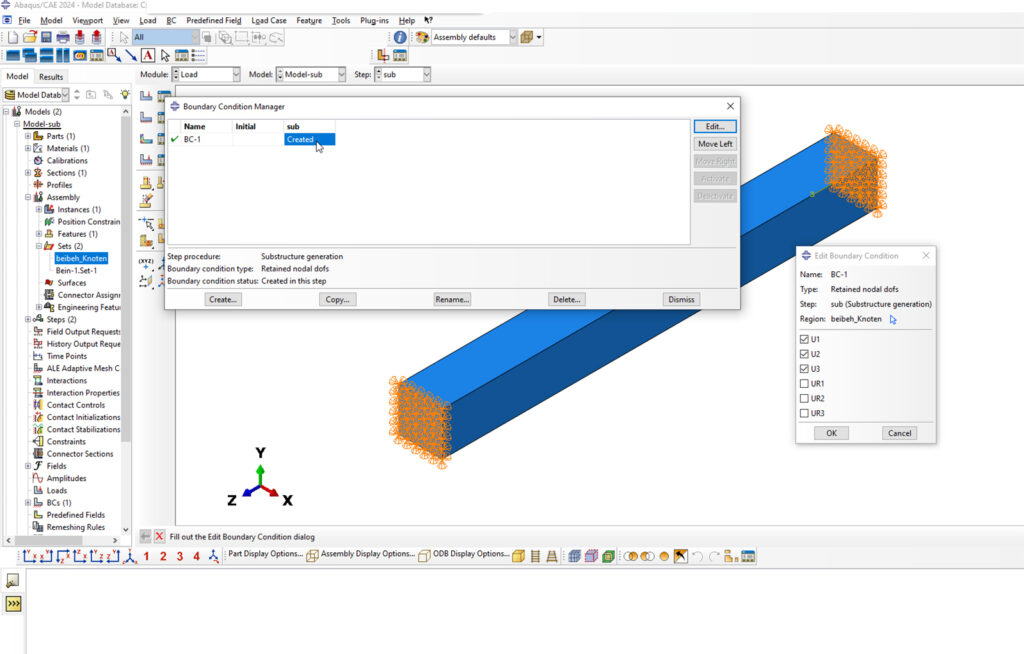
Abbildung 5: Substrukturtechnik FEM: Zuweisung der zu erhaltenden Knoten als Randbedingung

5. Job zum Ausführen der Berechnung erstellen

• Starten Sie einen Berechnungsjob mit dem Namen „sub“, um die Matrizen für Steifigkeit und Masse sowie die zugehörigen Dateien zu berechnen.

6. Neues Modell zur Berechnung des Ursprungsproblems erstellen (Modell Tisch)

• Geometrie und Materialdefinition
  Erstellen Sie im „PART“-Modul die Geometrie der Tischplatte. Definieren Sie die “Section” im „PROPERTY“-Modul und ordnen Sie das bereits definierte Material der  “Section” zu.

• Substruktur importieren
  Nach der Berechnung des ersten Modells für die Substruktur wird eine Datei im Format „sub_Z1.sim“ generiert (Schema: „<Jobname>_Z<Identifier>.sim“), die Sie im Modell mit der Tischplatte als „PART“ importieren.

• Zusammenbau
  Fügen Sie die Baugruppe im “ASSEMBLY”-Modul zusammen.

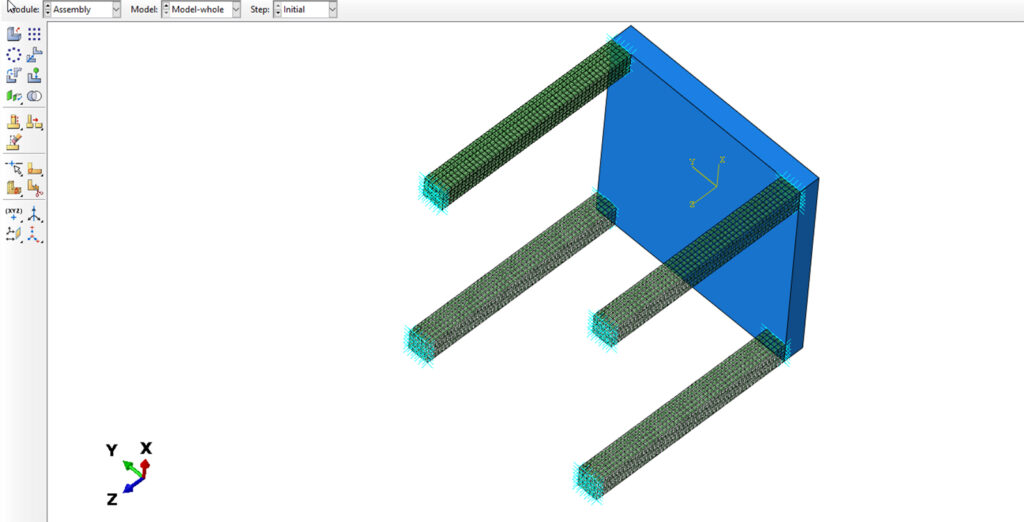
Abbildung 6: Substrukturtechnik FEM: Ansicht der Baugruppe mit Substrukturen

7. Lastschritt (Static General) und Randbedingungen definieren

• Interaktion. 
  Erstellen Sie einen „Tie“-Constraint zwischen den Schnittstellen der Tischplatte und den Tischbeinen. Diese Interaktion wird nur für die Knoten definiert, die Sie für das Hauptmodell behalten wollen.

• Bewegungssperre.
  Sperren Sie die translatorischen Freiheitsgrade der Knoten, die Sie am unteren Ende der Tischbeine behalten wollen.

• Last anwenden.
  Definieren Sie eine Drucklast auf die obere Seite der Tischplatte.

8. Field Output für Substrukturen definieren (bei Bedarf)

• Erstellen Sie im „STEP”-Modul ein „Field Output“ für die Substrukturen und wählen Sie die Variablen aus, die für die Substruktur relevant sind, wie z. B. die Spannungsverteilung in den Tischbeinen.

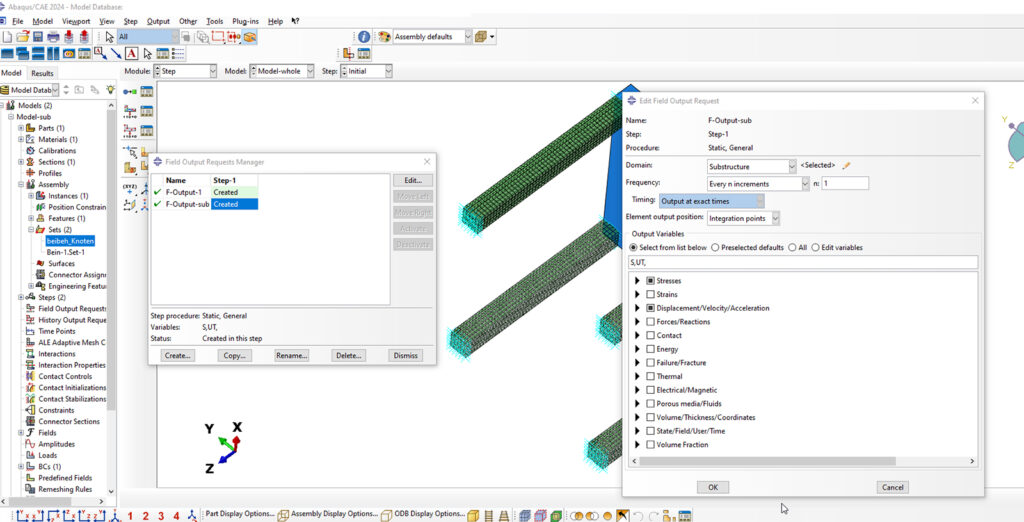
Abbildung 7: Substrukturtechnik FEM: Definition eines “Field-Ouputs” zur Ausgabe der Spannung in den Beinen

9. Vernetzung und Berechnung des gesamten Modells.

• Vernetzen Sie die Tischplatte, erstellen Sie den Berechnungsjob “general” und starten Sie die Berechnung des gesamten Modells.

10. Zusammenführen der Ergebnisse.

• Laden Sie die generierten ODB-Dateien für die Substrukturen (4x) und für das Gesamtmodell und kombinieren Sie diese zur Darstellung des Gesamtergebnisses.

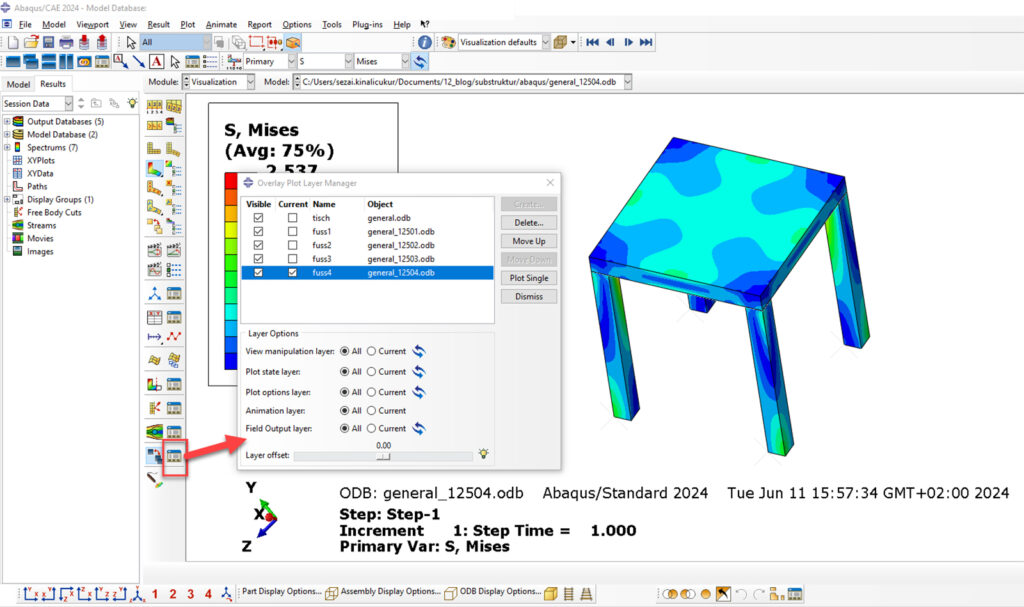
Abbildung 8 : Substrukturtechnik FEM: Überlagerung der Einzelergebnisse

Fazit 

Substrukturtechnik in SIMULIA Abaqus bietet Unternehmen eine effiziente Methode zur Reduzierung von Rechenzeit und Speicherbedarf bei komplexen Modellen. Durch die Aufteilung großer Strukturen in kleinere, wiederverwendbare Einheiten lassen sich Simulationen schneller und ressourcenschonender durchführen. SIMULIA Abaqus erleichtert die Modellierung, Vernetzung und Integration dieser Substrukturen und bietet damit eine flexible Lösung, um auch mit begrenzter Hardware präzise Ergebnisse zu erzielen. Für die Anwendenden bedeutet das weniger Zeit- und Kostenaufwand und mehr Flexibilität – ein klarer Vorteil und ein starkes Werkzeug für den Erfolg in der FEM-Analyse.