Tipps & Tricks
Erklärung der Singularitäten im Bereich FEM
WAS IST EINE FEM-SINGULARITÄT? In der Finite-Elemente-Methode (FEM) handelt es sich bei einer Singularität um eine Stelle in einem physikalischen Problem, an der eine oder mehrere Größen unendlich oder nicht definiert werden. Dies kann zu numerischen Problemen führen, da die Berechnungen im Zusammenhang mit Singularitäten besonders empfindlich sind und die Genauigkeit von Computersimulationen beeinträchtigen können. […]
21.05.24
WAS IST EINE FEM-SINGULARITÄT?
In der Finite-Elemente-Methode (FEM) handelt es sich bei einer Singularität um eine Stelle in einem physikalischen Problem, an der eine oder mehrere Größen unendlich oder nicht definiert werden. Dies kann zu numerischen Problemen führen, da die Berechnungen im Zusammenhang mit Singularitäten besonders empfindlich sind und die Genauigkeit von Computersimulationen beeinträchtigen können.
Singularitäten können in verschiedenen Kontexten auftreten, wie zum Beispiel in mechanischen oder thermischen Problemen. Ein häufiges Beispiel ist die Konzentration von Spannungen oder Deformationen an einer scharfen Ecke oder einem Punkt mit einer starken Geometrieänderung. Solche Stellen können in der FEM-Analyse schwierig zu handhaben sein, da sie zu ungewöhnlich großen Werten in den Ergebnissen führen können, die in der Realität nicht auftreten würden.
Um mit Singularitäten in der FEM umzugehen, gibt es verschiedene Ansätze. Eine Möglichkeit ist die Verfeinerung des Gitternetzes in der Nähe der Singularität, um eine bessere Auflösung zu erzielen. Eine andere Methode ist die Verwendung spezieller Techniken, um Singularitäten zu glätten oder zu vermeiden. Diese Techniken können je nach Anwendungsgebiet und Problemstellung variieren.
BEISPIELE VON SINGULARITÄTEN IN DER FEM
Im Bereich der FEM-Simulation spricht man von einer FEM-Singularität, wenn im Sinne von konstruktiven Bedingungen eines CAD-Modells oder von Modellbildungsmethoden sich folgende Zustände ergeben:
An eckigen Innenkonturen von Volumen-Elementen, Schalen-Elementen oder ebenen Elementen. Hierbei handelt es sich um ideal scharfe Kerben.
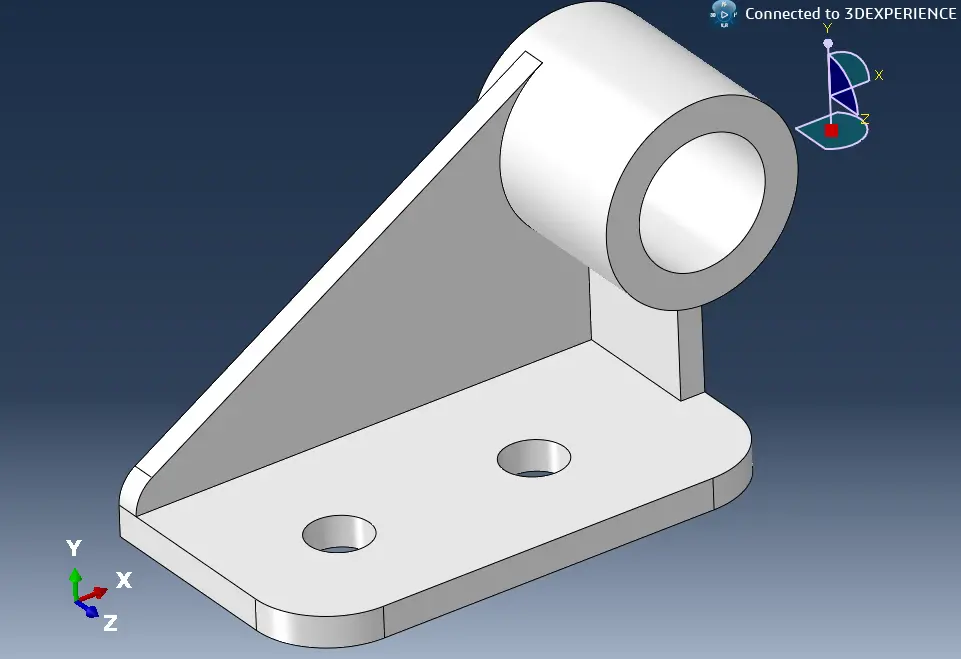

Verbindungsstellen zwischen unterschiedlichen Element-Typen, zum Beispiel Schalen-Element zu Balken-Element, Volumen-Element zu Balken-Element, Schalen-Element zu Volumen-Element.
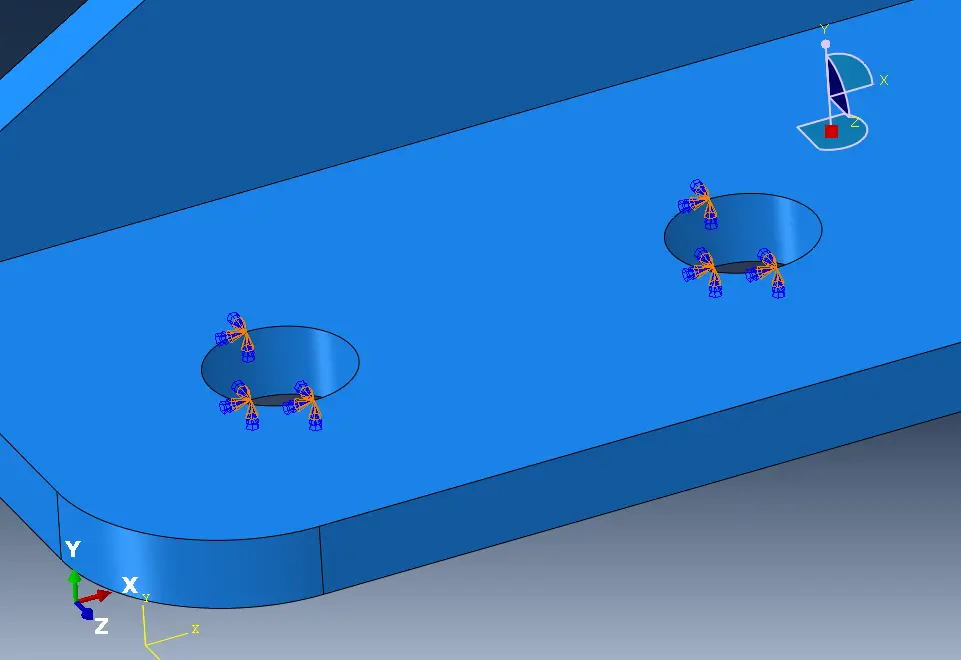
An Positionen, die mit einzelnen Kräften oder Linienkräften belastet sind.
Das Gleiche gilt an Grenzen oder harten Randbedingungen zwischen festgehaltenen und freien Elementbereichen.

An einer solchen Position, wo sich die Steifigkeit schlagartig ändert, ergeben sich im Modell bei der Auswertung unendlich hohe Spannungen.
Ein typisches Erkennungsmerkmal für eine Singularität ist, dass innerhalb eines Elements ein hoher Spannungsgradient auftritt.
In der Realität treten Singularitäten im theoretischen Sinne nicht auf, denn
jede Kerbe enthält in aller Regel eine Ausrundung, und
das Material plastifiziert lokal, wodurch sich die Spannungen abbauen und umverteilt werden.
Da beide Effekte in vielen FEM-Berechnungen (Modellvereinfachungen, lineares Materialverhalten) nicht berücksichtigt werden, wird mit zunehmender Netzdichte an dieser scharfkantigen Kerbe der unendlich hohe Spannungswert immer genauer, d.h. immer höher, berechnet. Das äußert sich darin, dass mit zunehmender Netzdichte der Spannungswert immer weiter ansteigt und keine Konvergenz erreicht wird. Eine allgemeine Genauigkeitsbetrachtung ist an diesen Stellen nicht sinnvoll und kann nicht ausgewertet werden. Hier soll auf einschlägige Literatur, auf Richtlinien oder Normen hingewiesen werden, wie mit benannten Stellen verfahren werden kann.
Kategorien
Allgemein Neuigkeiten Ratgeber Tipps & Tricks
Zum Bechtle PLM News-Service anmelden.
Keine Neuigkeiten, Tipps & Tricks, Events u.v.m. rundum Engineering & Manufacturing mehr verpassen.
Weitere Beiträge
Sie haben Fragen? Sprechen Sie uns an!
Wir sind hier, um Ihnen zu helfen! Schicken Sie uns Ihre Frage über das nebenstehende Formular.
Ihre Zufriedenheit hat oberste Priorität. Wenn Sie Informationen benötigen, Unklarheiten haben oder spezifische Anliegen besprechen möchten, zögern Sie nicht, uns zu kontaktieren. Füllen Sie einfach das Formular aus, wir werden uns schnellstmöglich bei Ihnen melden. Vielen Dank für Ihr Vertrauen!



